O(n) time complexity find longest palindromic substring
Translate
put origin string into a new char array, take “ABBABCBA”
make odd/ even length origin string into a odd length array (#,…,#)1
char S[] = {'^', '#', 'A', '#', 'B', '#', 'B', '#', 'A', '#', 'B', '#', 'C', '#', 'B', '#', 'A', '#', '\0'};
1 | char S[] = {'^', '#', 'A', '#', 'B', '#', 'B', '#', 'A', '#', 'B', '#', 'C', '#', 'B', '#', 'A', '#', '$'}; |
put position 0 and last postion a placeholder, S.length = origin * 2 + 3 odd length.
Mark
declare a array P[] to mark the S’s char symmetric radius length1
2char S[] = {'^', '#', 'A', '#', 'B', '#', 'B', '#', 'A', '#', 'B', '#', 'C', '#', 'B', '#', 'A', '#', '$'};
int P[] = { 0 , 1 , 2 , 1 , 2 , 5 , 2 , 1 , 4 , 1 , 2 , 1 , 6 , 1 , 2 , 1 , 2 , 1 , 0 };
describe:
array P used to describe radius, for example :
P[5] = 5 -> S(1,5) | S(5, 9)
calculate:
Declare varable
centerthe center of mirrorrightthe right terminal of mirror
right= center + P[center] , right point = center point + radiusleft= center - P[center] , left point = center point - radius
declareias current S cursor
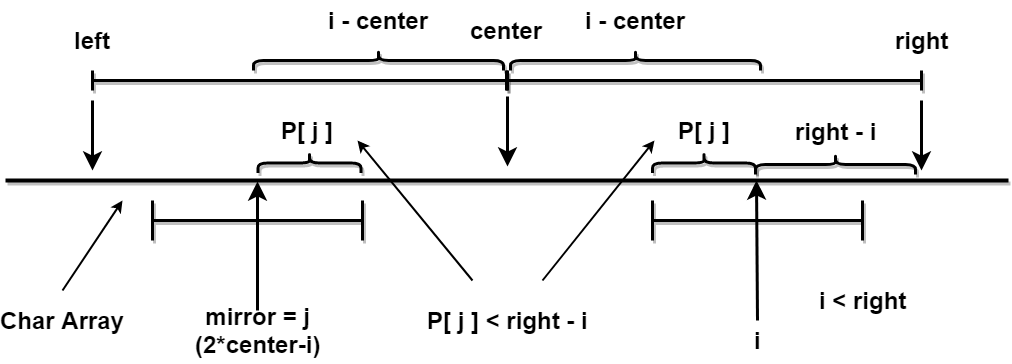
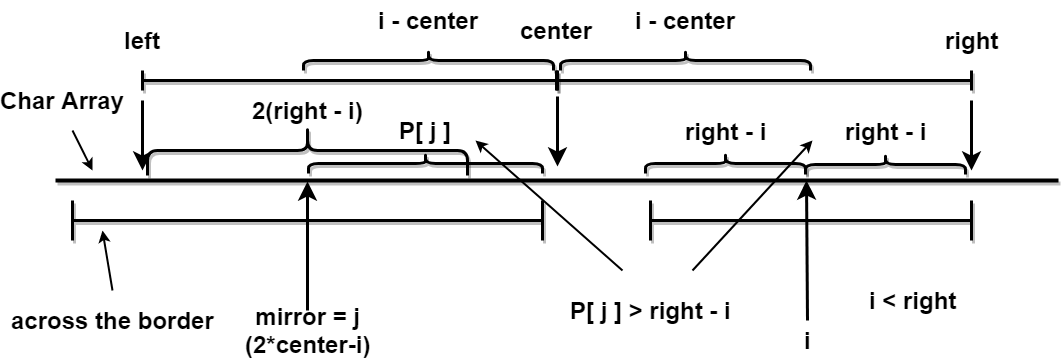
delcaremirroras the i’s mirror index ps. 2*center - right
when right > i, then P[i] >= Min(P[mirror], right - i)
- when
P[mirror]is minimum, that meaning P[mirror] < right - i
standard check block: (mirror - P[mirror], mirror + P[mirror]) | (i-P[mirror], i + P[mirror]) - when
right - iis minimum, that meaning P[mirror] > right - imirror - P[mirror]across the circle left border.
standard check block: (mirror - (right - i), mirrror + (right - i)) | (i - (right - i), right)
Code & Graph
1 | // right = center + P[center] |
Biggest value in P[] is longest palindromic substring lengh
It’s index is substring’s char center index.
1 | // find biggest value in P[] |