大家都知道,我们生活的世界是以运动和变化为主导的。地球绕着太阳转动;向上扔一块石头,它的速度会慢慢变小停下,然后返回地面,并且速度一直增加;印度的人口每年增加,并且增长的速度也在增加;放射性元素的衰变。这些都是无数现象中的沧海一粟,而数学是沟通和理解他们最自然的媒介。伽利略在三百多年前就说过,“大自然最伟大的书籍都被写进了数学符号里”
我们以微积分是什么以及它为什么的重要来这两个主题开始我们微积分之旅。鸟瞰前方的道路可以让我们清晰的看到目的和把握方向,还将让我们更好的理解许多技术细节,而这些技术细节做成了我们微积分课程的大体内容。
微积分通常分为两个部分,微分学和积分学。每部分都有各自的术语,繁多的符号和特定的计算方法。习惯这些需要大量的时间和练习,就像学习一门新语言一样。然而,这个事实不应把我们欺骗了,这门课核心问题真的很简单、很清晰,它们并不奇怪和神秘。
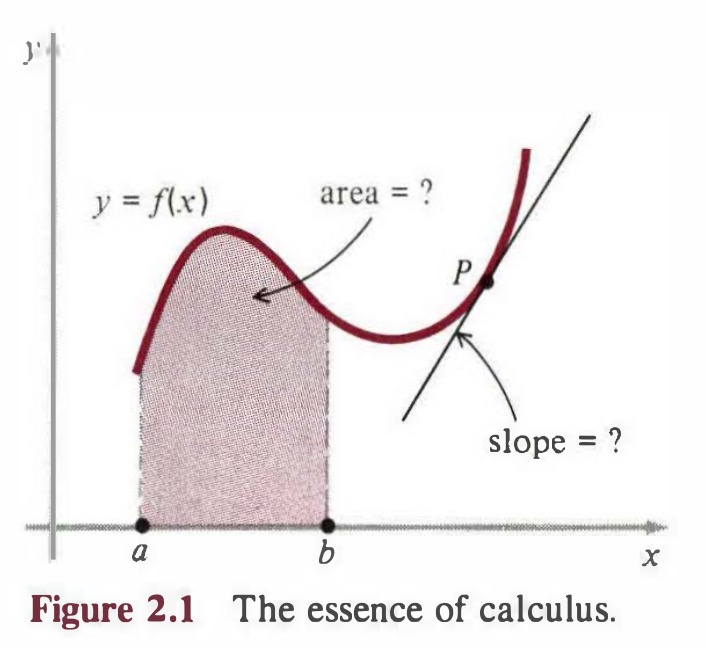
几乎所有微积分解决的问题和想法,都围绕着两个非常容易理解的几何问题。它们都是关于函数 $y=f(x)$ 的图形。为避免复杂性,我们假设图像完全在x轴之上,如图2.1所示。
- 问题一 基础微分问题,切线问题:计算切线在函数图像给定点 $P$ 上的斜率
- 问题二 基础积分问题,面积问题:计算在$x=a$、$x=b$之间 函数图像下的面积
乍一看这些问题看起来局限在斜率中。我们期望他们可以弄清楚几何上的显著特性,他们也做到了。令我们吃惊的是,他们也被用于许多重大而深远的各种科学中。微积分通过科学上的应用已经走出了数学的范围,我们主要目的之一是尽可能多的介绍他的广泛性。同时我们将不停强调几何和几何应用,基于这种方式可以让我们更容易理解微积分的思想。
人们有时候说微积分由十七世纪后期牛顿和莱布尼兹两个人发明的。实际上,微积分的产生经历了一个漫长的进化,它始于古希腊一直到十九世纪。牛顿和莱布尼兹确实很了不起,他们的贡献起着决定性的意义,但微积分并没有开始也没有结束。上文所述的问题深受十七世纪欧洲科学家的关注(尤其是费马),这两个天才用特殊的方法取得了突破性的进展。牛顿和莱布尼兹的成就就是认识到并探索了这些问题之间的联系,而其他任何人都不完全明白。具体来说,他们是最早掌握微积分基本定理的精髓,即是说,切线问题的解可用于解决面积问题。这个定理在整个数学来说非常重要,并且是由他俩独立发明的。他们和他们的继任者用它来衔接微分和积分,产生许多非凡的方法。
基于这些事实,我们从研究切线问题入手。然后,再转向面积问题。然后我们扩展我们的基本概念和工具到更广泛函数,这些函数被用于许多重要的应用中。
在尝试计算切线的斜率之前,我们首先得定义切线是什么,这看起来并不容易。
对圆来说这并不困难,圆的切线就是与圆只有一个交点的直线,这个点叫做切点;而其余的直线要么有两个交点,要么没有交点。这种情况给我们提供了非常直观的想法,我们可以在曲线上给定一个点,在那个点处与曲线相交得到的线就是切线。还有种定义是与曲线只相交于一点的线。这一定义被希腊人用于处理圆和一些特殊的曲线,但一般情况下,这个定义并非对所有曲线成立。考虑图1的曲线:下面那条线是切线,但是不满足定义。上面那条线满足定义,但明显不适切线。

Figure 2.2
切线的现代概念由费马提出。之后我们会看到,这个概念不仅是对切线几何性质和油的说明,也是构造切线的关键。
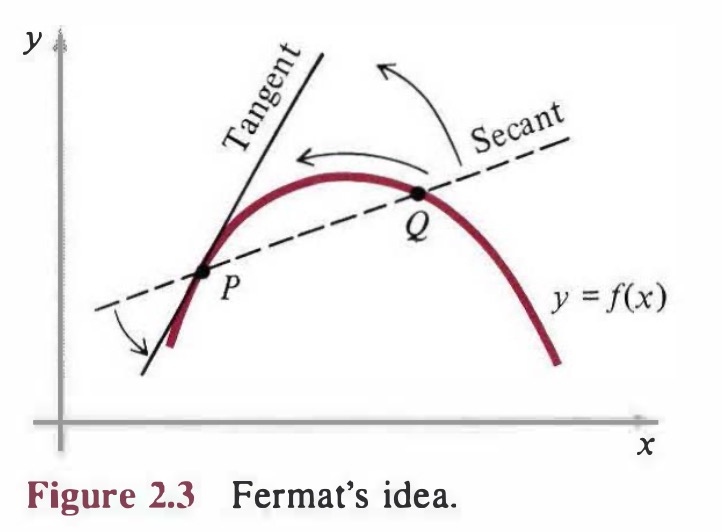
简单地说,想法是这样的:考虑曲线 $y:f(x)$,$P$ 是给定的点 (图2.3)。 $Q$ 是曲线上临近的点,绘制割线 $PQ$ 。点 $P$ 的切线可以看作随着 $Q$ 沿曲线移向P时割线的极限位置。之后我们会看到这个定性的想法是如何产生计算函数 $f(x)$ 切线斜率的定量方法。
对此不要有任何误解。不要小觑这种切线的思维方式。相反地,它是数学中几个最富有成效想法中的一个,没有它,就没有物理学中的速度或加速度,没有牛顿动力学或天文学,没有任何形式的物理学,只有现象的口头描述而已,当然也不会有现在的工业时代。